Steamをインストール
ログイン
|
言語
简体中文(簡体字中国語)
繁體中文(繁体字中国語)
한국어 (韓国語)
ไทย (タイ語)
български (ブルガリア語)
Čeština(チェコ語)
Dansk (デンマーク語)
Deutsch (ドイツ語)
English (英語)
Español - España (スペイン語 - スペイン)
Español - Latinoamérica (スペイン語 - ラテンアメリカ)
Ελληνικά (ギリシャ語)
Français (フランス語)
Italiano (イタリア語)
Bahasa Indonesia(インドネシア語)
Magyar(ハンガリー語)
Nederlands (オランダ語)
Norsk (ノルウェー語)
Polski (ポーランド語)
Português(ポルトガル語-ポルトガル)
Português - Brasil (ポルトガル語 - ブラジル)
Română(ルーマニア語)
Русский (ロシア語)
Suomi (フィンランド語)
Svenska (スウェーデン語)
Türkçe (トルコ語)
Tiếng Việt (ベトナム語)
Українська (ウクライナ語)
翻訳の問題を報告
















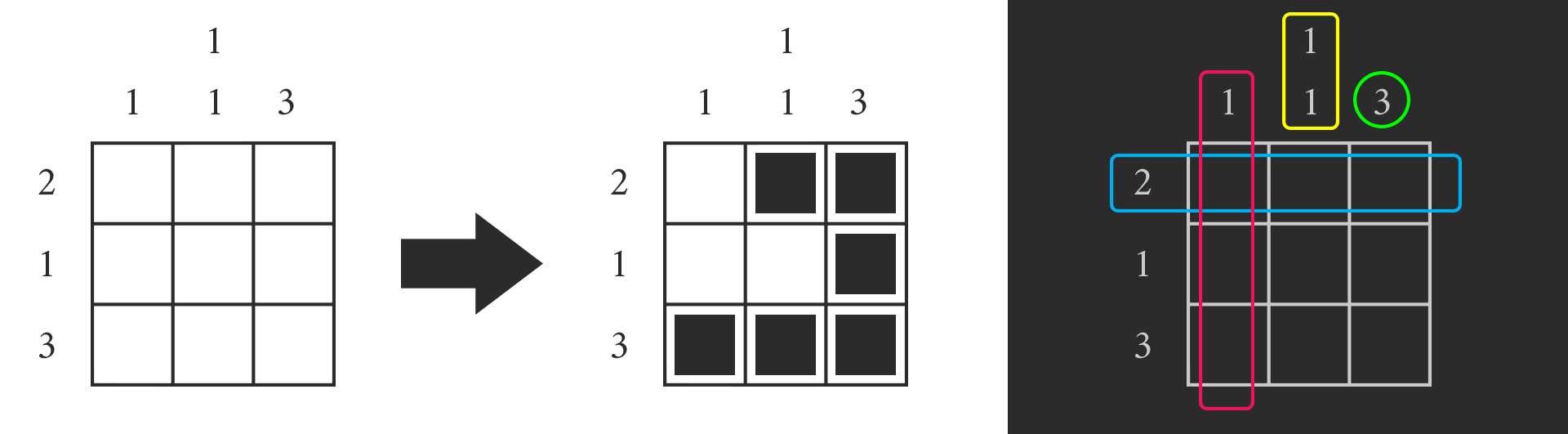


 Steam
Steam @steam
@steam